Paradojas de Zenón

Imagina que Aquiles, un corredor muy rápido, está en una carrera con una tortuga. Como Aquiles corre mucho más rápido, le da una ventaja a la tortuga y la deja empezar primero. Ahora, piensa en lo siguiente:

1. Cuando Aquiles llega al lugar donde estaba la tortuga al principio, la tortuga ya ha avanzado un poquito más.
2. Cuando Aquiles llega a ese nuevo lugar donde está la tortuga, ella se ha movido un poquito más otra vez.

Y así sigue, Aquiles siempre llega a donde estaba la tortuga antes, pero cuando llega, ella ya ha avanzado un poco más. Parece que nunca podrá alcanzarla, porque siempre hay un pedacito de distancia que aún falta, aunque sea muy pequeño.

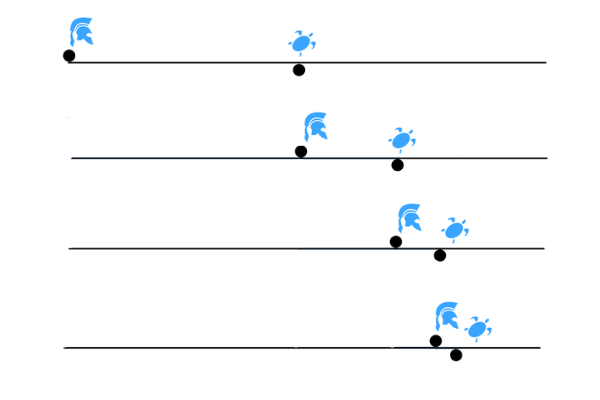
1. La tortuga tiene una ventaja inicial, supongamos que 10 metros.
2. Cuando Aquiles recorre esos 10 metros, la tortuga avanza un poquito más, digamos 1 metro.
3. Aquiles corre esos 1 metro y, cuando llega, la tortuga ha avanzado un poco más, digamos 0.1 metros.
4. Aquiles corre esos 0.1 metros y, cuando llega, la tortuga ha avanzado 0.01 metros, y así sucesivamente.

Cada vez que Aquiles alcanza el punto donde estuvo la tortuga antes, la tortuga ha avanzado una distancia más pequeña, pero nunca llega a recorrer una distancia infinita. La suma de todas esas pequeñas distancias es finita. En otras palabras, aunque parezca que hay una cantidad infinita de pasos que Aquiles debe dar, la distancia total que tiene que recorrer es finita.

Por lo tanto, Aquiles sí alcanzará a la tortuga en un momento, aunque las distancias sean cada vez más pequeñas. Esto se debe a que la serie de distancias que debe recorrer (10, 1, 0.1, 0.01, ...) suma un número finito. Aquiles alcanzará a la tortuga en algún momento.

Suma de infinitos números

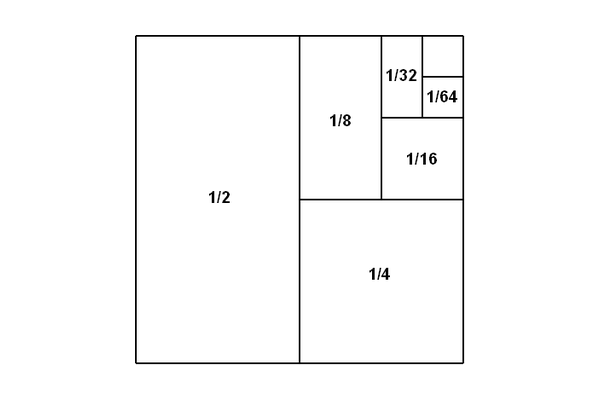
Cuando sumamos números infinitos, a veces el total puede ser finito (como en la Paradoja de Aquiles y la tortuga). Otro ejemplo es el caso de la suma 1/2 + 1/4 + 1/8 + 1/16 + …. En este ejemplo, cada número es más pequeño que el anterior: 1/2 es la mitad de 1, 1/4 es la mitad de 1/2, 1/8 es la mitad de 1/4, y así sucesivamente. Aunque hay infinitos términos en esta suma, cada número es cada vez más pequeño y se acerca a cero.

Lo interesante de esta suma es que, aunque nunca terminamos de sumar (ya que hay infinitos términos), el total se puede calcular. La suma de todos estos términos es 1. Esto ocurre porque cada vez que sumamos un término más pequeño, la cantidad que sumamos disminuye mucho. Si sumamos suficientes términos, nos acercamos tanto a 1 que, en realidad, nunca necesitamos sumar todos los términos para llegar a ese resultado. Matemáticamente, esto se llama serie geométrica y, cuando el número que multiplicamos por cada término (en este caso, 1/2) es menor que 1, la suma total siempre tiene un resultado finito. Así, aunque haya infinitos términos, el total sigue siendo 1.

La siguiente ilustración muestra gráficamente la suma.